lstm
标签:lstmLSTM 的优势
LSTM 是 Sepp Hochreiter 和 Jürgen Schmidhuber 在上世纪九十年代中期提出的,它可以解决梯度消失的问题,这一问题是影响 RNN 表现的重大障碍。
LSTM 还可保留误差,用于沿时间和层进行反向传递。LSTM 将误差保持在更为恒定的水平,让 RNN 能够进行许多个时间步的学习(超过 1000 个时间步),从而打开了建立远距离因果联系的通道。
LSTM 将信息存放在递归网络正常信息流之外的门控单元中。这些单元可以存储、写入或读取信息,就像计算机内存中的数据一样。单元通过门的开关判定存储哪些信息,以及何时允许读取、写入或清除信息。但与计算机中的数字式存储器不同的是,这些门是模拟的,包含输出范围全部在 0~1之间的 sigmoid 函数的逐元素相乘操作。相比数字式存储,模拟值的优点是可微分,因此适合反向传播。
这些门依据接收到的信号而开关,而且与神经网络的节点类似,它们会用自有的权重集对信息进行筛选,根据其强度和导入内容决定是否允许信息通过。这些权重就像调制输入和隐藏状态的权重一样,会通过递归网络的学习过程进行调整。也就是说,记忆单元会通过猜测、误差反向传播、用梯度下降调整权重的迭代过程学习何时允许数据进入、离开或被删除。
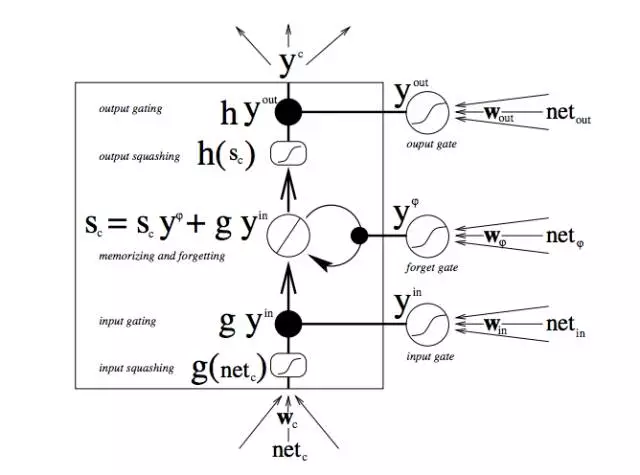
首先,最底部的三个箭头表示信息从多个点流入记忆单元。当前输入与过去的单元状态不只被送入记忆单元本身,同时也进入单元的三个门,而这些门将决定如何处理输入。
图中的黑点即是门,分别决定何时允许新输入进入,何时清除当前的单元状态,以及/或何时让单元状态对当前时间步的网络输出产生影响。S_c 是记忆单元的当前状态,而 g_y_in 是当前的输入。记住,每个门都可开可关,而且门在每个时间步都会重新组合开关状态。记忆单元在每个时间步都可以决定是否遗忘其状态,是否允许写入,是否允许读取,相应的信息流如图所示。
图中较大的黑体字母即是每项操作的结果。
下面是另一张图,将简单 RNN(左)与 LSTM 单元(右)进行对比。蓝线可忽略;图例有助理解。
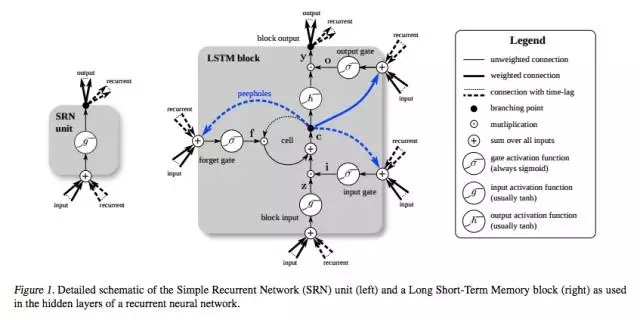
应当注意的是,LSTM 的记忆单元在输入转换中给予加法和乘法不同的角色。两张图中央的加号其实就是 LSTM 的秘密。虽然看起来异常简单,这一基本的改变能帮助 LSTM 在必须进行深度反向传播时维持恒定的误差。LSTM 确定后续单元状态的方式并非将当前状态与新输入相乘,而是将两者相加,这正是 LSTM 的特别之处。(当然,遗忘门依旧使用乘法。)
不同的权重集对输入信息进行筛选,决定是否输入、输出或遗忘。遗忘门的形式是一个线性恒等函数,因为如果门打开,则记忆单元的当前状态就只会与 1 相乘,正向传播一个时间步。
此外,讲到简单的窍门,将每个 LSTM 单元遗忘门的偏差设定为 1,经证明可以提升网络表现。
关于梯度消失的解决,可以参考知乎:LSTM如何来避免梯度弥散和梯度爆炸?
- An Empirical Exploration of Recurrent Network Architectures
- Empirical Evaluation of Gated Recurrent Neural Networks on Sequence Modeling
另外,梯度爆炸问题,lstm无法解决,需要通过梯度cliping来解决(On the difficulty of training Recurrent Neural Networks)
原创文章,转载请注明出处!
本文链接:http://hxhlwf.github.io/posts/dl-lstm.html