基于深度学习的ctr预估模型集合(持续更新)
标签:ctr模型, deepFM, wide & deep, deep & cross, ffm, fm, fnn, pnn, snn, ccpm, opnn, nfm, afm目录
参考: 深度学习在 CTR 中应用
基于lr和gbdt的可以参考传统ctr预估模型
FM
二阶多项式模型:
\[
\phi(x) = w_0+\sum _{i}w_ix_i+\sum_{i}\sum_{j<i}w_{ij}x_ix_j
\]
多项式模型的问题在于二阶项的参数过多,假设特征个数为n,那么二阶项的参数数目为n(n+1)/2,参数太多,而却只有少数模式在样本中能找到,因此模型无法学出对应的权重。
FM模型:
\[
\hat{y} = w_0+\sum _{i=1}^nw_ix_i+\sum_{i=1}^{n-1}\sum_{j=i+1}^{n}\left \langle \mathbf{v}_i,\mathbf{v}_j \right \rangle x_ix_j
\]
其中,
\(w_0\in \mathbb{R}\)\(\mathbf{w}\in \mathbb{R}^n\)\(\mathbf{V}\in \mathbb{R}^{n\times k}\)\(\hat{w_{ij}}=\mathbf{v}_i\mathbf{v}_j^T=\sum _{l=1}^kv_{il}v_{jl}\)所以上式中的\(\mathbf{v}_i\)就表示\(\mathbf{V}\)这个矩阵的第i行(有k列),而\(\left \langle \mathbf{v}_i,\mathbf{v}_j \right \rangle\)就表示第i行和和j行这两个向量的内积(得到一个数),而得到的正好就是权重矩阵的第i行第j列的元素\(\hat{w}_{ij}\),而\(\hat{w}\)这个矩阵是\((n-1)\times(n-1)\)维的矩阵,刻画的是相邻两个x【\(x_i\)和\(x_{i+1}\)】之间的系数。因此,可以理解为,将这个\((n-1)\times(n-1)\)维的矩阵用一个\(n\times k\)维的低秩矩阵来表示。
FFM
FNN, SNN
FNN
SNN
CCPM
A Convolutional Click Prediction Model
PNN
Product-based Neural Networks for User Response Prediction
IPNN
OPNN
Wide & Deep
Wide & deep learning for recommender systems
LR 对于 DNN 模型的优势是对大规模稀疏特征的容纳能力,包括内存和计算量等方面,工业界都有非常成熟的优化方法; 而 DNN 模型具有自己学习新特征的能力,一定程度上能够提升特征使用的效率, 这使得 DNN 模型在同样规模特征的情况下,更有可能达到更好的学习效果。
模型结构如下:
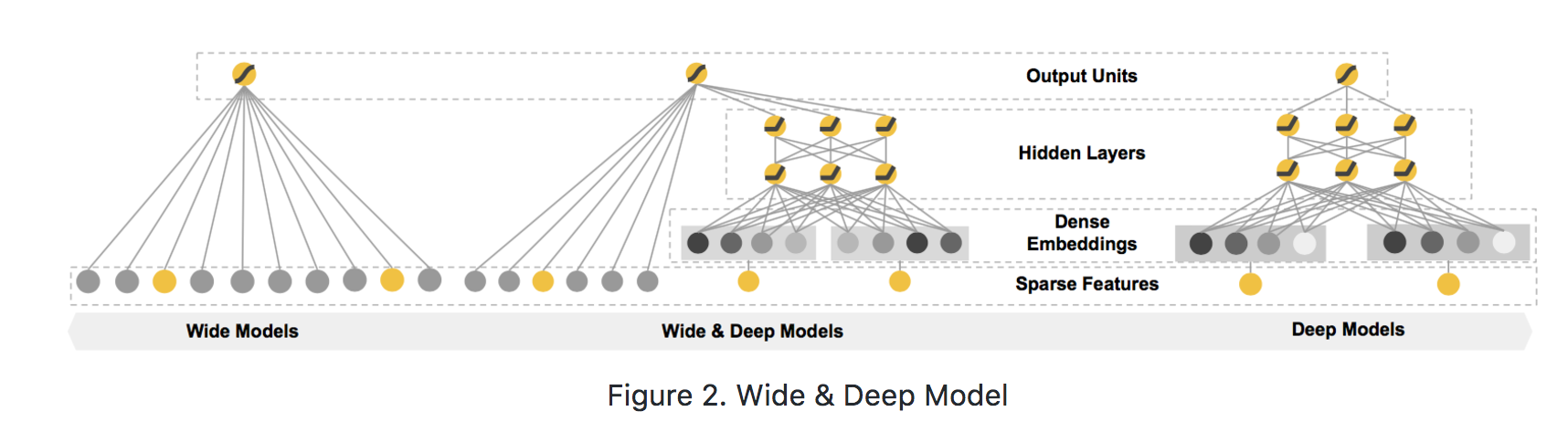
模型左边的 Wide 部分,可以容纳大规模系数特征,并且对一些特定的信息(比如 ID)有一定的记忆能力; 而模型右边的 Deep 部分,能够学习特征间的隐含关系,在相同数量的特征下有更好的学习和推导能力。
用于ctr预估https://github.com/PaddlePaddle/models/tree/develop/ctr
特征的生成:https://github.com/PaddlePaddle/models/blob/develop/ctr/dataset.md
DeepFM
DeepFM: A Factorization-Machine based Neural Network for CTR Prediction
Deep & Cross
论文地址:deep & cross network for ad click predictions
参考:https://daiwk.github.io/posts/dl-deep-cross-network.html
NFM
Neural Factorization Machines for Sparse Predictive Analytics
AFM
Attentional Factorization Machines:Learning theWeight of Feature Interactions via Attention Networks
原创文章,转载请注明出处!
本文链接:http://hxhlwf.github.io/posts/dl-dl-ctr-models.html